STANDARDIZATION OF MILK USING PEARSON’S SQUARE METHOD
Compiled & Edited by-DR RAJESH KUMAR SINGH ,JAMSHEDPUR,JHARKHAND, INDIA, 9431309542,rajeshsinghvet@gmail.com
Milk standardization is important in the dairy industry because it is used to ensure that every consumer gets milk with constant fat content and consistency. Primarily, milk may be separated into two products; cream with high fat content (about 40% fat) and skimmed milk (about 0.03% fat) using a centrifugal separator.
The process of standardization involves reduction of fat content in milk from the natural minimum of 3.25%. The cream extracted from the standardization process facilitates processing of other dairy products such as ice cream, butter, and ghee.
Milk standardization can take two forms i.e. either partial separation or mixing of skimmed and whole milk. Mass balancing plays a key role in successful standardization of milk.
STANDARDIZATION OF MILK
Many dairy processes require standardization of the chemical composition of milk meant for market purpose or milk products manufacture. Standardizing milk might require control of only one component (usually fat) while allowing the others to vary or control two or more components simultaneously.
Standardization———-
It may be defined as the adjustment of one or more of the milk constituents to a nominated level. In market milk industry, this normally involves reducing the butterfat content by addition of skim milk or through the removal of cream.
Objectives
• To comply with the legal requirements for particular milk/dairy products.
• To provide the consumer with a uniform product.
• To ensure economics in production.
Addition of skim milk increases the volume of milk available for sale and removal of cream allows the production of other value added dairy products such as table cream, butter or other high fat products.
Methods of Calculation
For standardization of milk or cream for product manufacture, usually the proportions of the various ingredients of known composition to be mixed, is required to be estimated. This can be done by:
• Pearson’s Square method
• Algebraic equations
Pearson’s square method
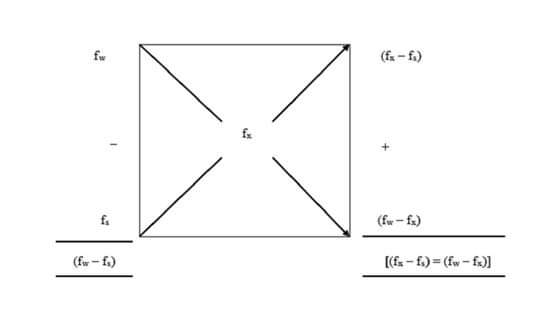
Draw a square and place in the centre of it the desired fat percentage. Place at the left hand corners of the square, the fat percentage of the materials to be mixed. Next, subtract the number in the centre from the larger number at the left hand side of the square and place the remainder at the diagonally opposite right hand corners. The number on the right hand side now represents the number of parts of each of the original materials that must be blended to have the desired fat content in resultant mix. The number at the upper right corner refers to the parts of material whose fat test was placed at the upper left corner and the number at the lower right corner refers to the parts of material whose fat test was placed at the lower left corner. If the numbers on the right are added, the sum obtained will represent the parts of the finished product.
Examples
Problem 1
600 kg of cow milk testing 4% fat is to be standardized to toned milk by removing 33% fat cream. Calculate the amount of toned milk.
Solution
A = Fat percentage of cow milk = 4%
B = Fat percentage of cream = 33%
E = Fat percentage of toned milk = 3%
Calculation
30 kg of cow milk requires removal of 1 kg of cream
So, 1 kg of milk requires removal of 1/30 kg of cream
Therefore, 600 kg milk will require removal of (1/30 x 600) = 20 kg cream
So, the amount of toned milk will be (600 – 20) = 580 kg.
Proof Sheet
In order to check the accuracy of calculations made, put the calculated values of various raw materials in the below given format and check:
In the product, fat required = 580 * (3/100) = 17.4 kg
Hence proved, because the required value is equal to the calculated value (in the table).
Problem 2
1000 kg of double toned milk (DTM) is to be prepared by mixing whole milk, testing 5.5% fat and skim milk testing 0.2% fat. Calculate the amount of whole milk and skim milk required.
Solution
A = Whole milk fat content = 5.5 %
B = Skim milk fat content = 0.2 %
E = Required percentage of fat in double toned milk = 1.5%
So, C = A – E = 5.5 – 1.5 = 4.0 kg skim milk
D = E – B = 1.5 – 0.2 = 1.3 kg whole milk
Calculation
DTM quantity = 4 kg + 1.3 kg = 5.3 kg
To prepare 5.3 kg of DTM, whole milk required = 1.3 kg.
Therefore, to prepare 1000 kg of DTM, whole milk required will be = (1.3/5.3) x 1000 = 245.28 kg whole milk
To prepare 5.3 kg of DTM, skim milk required is 4 kg.
So, to prepare 1000 kg of DTM, we require – (4/5.3) x 1000 = 754.72 kg skim milk
The required quantity of whole milk is 245.28 kg and the skim milk is 754.72 kg for preparation of 1000 kg of DTM.
Problem 3
200 kg milk testing 7.2% fat is to be standardized to 4.5% fat by addition of skim milk testing 0.1% fat. Calculate the amount of skim milk required?
A = Fat in whole milk = 7.2%
B = Fat in skim milk = 0.1%
C = A – E = 7.2 – 4.5 = 2.7 kg skim milk
D = E – B = 4.5 – 0.1 = 4.4 kg whole milk
E = Fat percentage of standardized milk, 4.5%
Solution
Here,
fat % of given milk A = 7.2
Fat % of skim milk B = 0.1%
Fat % of standardized product E = 4.5%
So, C = A – E = 7.2 – 4.5 = 2.7 kg of skim milk
D = E – B = 4.5 – 0.1 = 4.4 kg of whole milk
So, here standardized milk is prepared by mixing whole milk and skim milk
E = C + D = 2.7 + 4.4 = 7.1 kg of standardized milk.
To prepare 7.1 kg of standardized milk, given whole milk required is 4.4 kg.
So, to prepare 200 kg of standardized milk, it requires (4.4/7.1) x 200 = 123.94 kg whole milk.
7.1 kg of standardized milk requires 2.7 kg skim milk.
So, to prepare 200 kg of standardized milk, it requires (2.7/7.1) x 200 = 76.00 kg skim milk.
The required quantity of skim milk is 76.00 kg for preparation of 200 kg of standardized milk testing 4.5% fat.
Algebraic equations
In this method, we should know the composition of the products to be mixed, the final product and the quantity of any one product. Mass balance equations are formed and solved.
The formula for determining the quantities of skim milk and raw milk on this basis is as follows:
• Skim milk (kg) = kg standard milk required x (% fat in raw milk – % fat in standard milk)
• Whole milk (kg) = kg standard milk required x (% fat in standard milk – % fat in skim milk)
Problem
Prepare 500 kg milk testing 3.0% fat and 8.5% SNF. You are provided with whole milk having 5.0% fat and 9.0% SNF and skim milk powder having 0.5% fat and 96.0% SNF.
Solution
Let the quantity of the whole milk = X kg
Quantity of SMP = Y kg
Quantity of water = Z kg
Fat equation:
X + Y + Z = 500
Now, solving equations (1) and (2) by 5, we get,
SNF required = 500 * (8.5/100) = 42.5 kg
Hence proved, because the required values are equal to the calculated values (in the table).
Example 4
2000 kg of milk (with 87.6% water, 3.8% fat, 3.2% protein, 4.6% lactose, and 0.7% ash content) has to be reduced in fat content from 3.8% to 2.5% by removal of cream with 40% fat content from the milk. How much milk will have to be removed?
Solution.
TMB: 2000 = C + M
FMB: 20000.038 = 0.4C + 0.025M 20000.025 = 0.025C + 0.025M
Solving the equations will give the values of C = 69.3 kg and the remaining milk M = 1930.7 kg.
Example 2
If 3000 kg of the same milk used in the previous example is separated into cream with 45% fat and skimmed milk with 0.05% fat, how much cream and skimmed milk are expected assuming no losses?
Solution
TMB: 3000 = C + M
FMB: 30000.038 = 0.45C + 0.0.0005*S
Solving the equations will give C = 250.3 kg and S = 2749.7 kg
Example 5
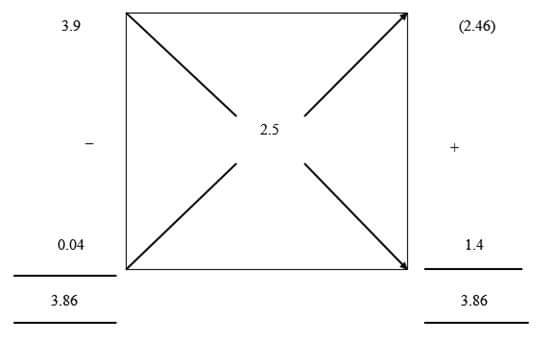
How much whole milk with 3.9% fat and skimmed milk with 0.04% fat content will you need to produce 2000 kg of standardized milk with 2.5% fat?
Solution:
Using mass balance method:
TMB: W + S = 2000
FMB: 0.039W + 0.0004S = 0.025*2000
Solving for W = 1274.6 kg and S = 725.4 kg
Using Pearson’s Square method:
Proportion of the whole milk = 2.46/3.86
Amount of whole milk required = (2.46/3.86)2000 = 1274.6 kg Proportion of skimmed milk = 1.4/3.86 Amount of skimmed milk required = (1.4/3.86)2000 = 725.4 kg (or 2000 – 1274.6)
Reference-On Request